If you haven't seen A Beautiful Mind, then you may think the term "Game Theory" sounds like some geeky over-interpretation of video game strategies, but it is in fact a complex mathematical discipline that has a wide-ranging array of real-life applications.

While many adults might not think a "game" is a very serious term, in the context of Game Theory it refers to a scenario that can be either competitive (where there are clear winners and losers) or cooperative (where the goal is to maximize benefit for all players).

One of the more famous scenarios is called the "prisoner's dilemma", and is a good example of a competitive game. Once you understand this game, you will start seeing it everywhere in life, and it can even begin to affect your decision-making.

The great thing about the prisoner's dilemma is even though there is some complex math associated with it, you really only need to understand basic addition in order to grasp the main takeaways. So if you don't consider yourself mathematically gifted, never fear! I'll try to make it as simple as possible.

Let's dive in...

What Is The Prisoner's Dilemma?

Imagine, if you will, that you have been arrested for a fairly benign crime, say something like selling drugs. At the same time that you were arrested, someone else (for whom you do not have any loyalty) was also arrested for a similar crime. You are each being held in separate cells and cannot communicate with one another. The attorney general comes into your cell and begins to talk. He lets you know that for the crime you have been arrested, the sentence is 2 years in prison. What you don't know is that the attorney general has a hunch that you and the other prisoner were accomplices in a past bank robbery, but he has no evidence for his hunch. The only way he can convict either prisoner for the bank robbery is if they confess, so he has an idea...

He tells you that if you confess to the bank robbery and the other prisoner doesn't, then you don't have to go to prison for your previous sentence, meanwhile, the other prisoner will serve 10 years. Of course, this works the other way too, if the other prisoner confesses and you don't, then YOU serve 10 years and they walk free. If you both confess, then you both serve 6 years in prison.

What do you do?

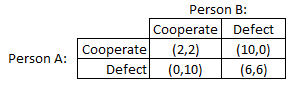
It's easiest to break the situation down into a table, like I've done below. Each cell has the costs associated with each decision. From now on, we will use the term "cooperate" to refer to the prisoner cooperating with the other prisoner and not confessing, and the term "defect" to refer to the prisoner confessing.

As you can see, there is symmetry to the table, because the costs associated with defecting are the same for both prisoners. Now, there is some math that goes into what is the "correct" decision for each prisoner, and the costs associated with each decision can have an effect on it. In different things I've read about the prisoner's dilemma, the jail sentences are not always the same. Sometimes, the sentence of defecting if the other prisoner cooperates is 1 year instead of 0, but that isn't all the important. What is important is the relative cost of each outcome, i.e. in the traditional sense, the cost of mutual cooperation is more than if one person defects, and the cost of mutual defection is less for each than if they cooperate and the other defects.

Which brings us back to: what is the right decision? If you look at it from a standpoint of win maximization, then it is tempting to say that the case where each prisoner cooperates is the overall best outcome. This is because in that case, each prisoner serves 2 years (for a total of 4 years). In the case of asymmetrical defection, the one prisoner serves 10 years (which is, as I learned in kindergarten, more than 4 years). The case of mutual defection is the worst, as each prisoner serves 6 years, for a total of 12.

This is a jail in Cork, Ireland that looks like a castle. Kinda spooky
Image Credit

Here is the important part of this thought experiment though: it is assumed that the prisoners have no loyalty to each other. With this in mind, each prisoner brings an element of selfishness to the table. The goal for each prisoner is not to reduce the overall amount of years that they both spend in prison, it's to reduce the amount of years that they individually spend in prison. If I'm in the cell, then I don't care how long the other guy is in prison, I just want to get out ASAP. More importantly, I have to assume that the other prisoner doesn't care how long I spend in prison, either.

Which brings us to the answer: the most logical thing to do is defect. Why? Because if you defect, then you get the best outcome regardless of the other prisoner's choice. Let's look at this for each case: if the other prisoner cooperates, then you are looking at either 2 years in prison for also cooperating, or 0 years in prison for defecting. In that case, you get out of prison earlier if you defect. In the other case, if the other prisoner defects, and you cooperate, then you spend a whopping 10 years in prison. If you defect, then you spend 6 years. Again, defecting gives you a shorter sentence.

This probably seems cold and selfish, and that's because it is, but if you are looking down the barrel of possibly 10 years in prison, then being nice isn't really a luxury that you can afford.

Of course, if both prisoners realize this, then it's highly likely that they both defect, and thus both spend 6 years in prison. This state (the bottom right square on the chart) is known as a "Nash Equilibrium", named after the guy from A Beautiful Mind. It's a stable condition that the system will reach if all players are playing logically.

The state at the top left of the chart, in which both prisoners cooperate, is an unstable condition. Because the incentive for each prisoner to defect is so great, even if they initially decide to be nice, it's likely that the longer they have to think about it, the more likely they will be to defect.

Some Takeaways

This article will be the first of several about the prisoner's dilemma. In subsequent articles, I'll choose a real-life example and dive into how it mirrors the prisoner's dilemma and how we can learn from the prisoner's dilemma to affect our choices.

The main points of the prisoner's dilemma (in the classic sense that I have outlined) are enumerated below:

• Two or more players (with questionable loyalty to each other)
• A slight reward for cooperating with each other
• A bigger reward for defecting if the other cooperates
• A large punishment for cooperating if the other defects
• A medium punishment for mutual defection

Here's a fun real-life example: athletes using steroids. Say there are two athletes who have about the same level of skill. They play in a sport in which performance enhancing drugs are illegal because they have long-term health consequences. While the athletes are concerned about this, their main concern is being the best athlete, because that's what pays the bills now. If neither of them takes steroids, then they won't have an advantage over each other, and won't have to deal with any long-term health consequences. If, however, one of them takes steroids and the other doesn't, then the one who juiced will have a significant advantage. If they both take steroids, then they still won't have an advantage over each other, but will also have to deal with the health consequences. Since the case in which they both take steroids is the "Nash Equilibrium" condition, it's very likely that they both choose to take steroids.

As you can see with this example, the prisoner's dilemma has kind of a depressing takeaway: more than likely, a game will devolve into a state in which every player is worse off than they previously were because they pursued a better outcome. It's both a lesson in morality and a lesson in human nature. If we were all selfless and pursued the best interests of everyone involved, then it's likely that everyone would be better off. Unfortunately, because we know that people are not selfless, we inevitably resort to our logical senses, and end up making life worse for everyone.

Once you start to figure out what makes the prisoner's dilemma tick, you can start to see it in a bunch of other situations. Which ones can you think of? Stay tuned for the ones I've thought about.