Over the holidays I helped my dad make some BBQ using his new smoker, and it turned out really well!

This wasn't ours, but it looked kind of like this!
Image Credit
Smoking a pork shoulder isn't too terribly difficult, the tricky part is getting the smoker set up so that the temperature is stable, getting the rub on the meat right, and then just being patient enough to wait however many hours it takes to cook.
During the time it was cooking, we had a temperature probe in the pork so that we could monitor its progress while cooking. At one point, about halfway through the cooking process, I was afraid that the temperature of the smoker was too hot, because I knew that it had several more hours to cook and the temperature of the meat was well over halfway to the final doneness temperature.
And that got me thinking, what should the temperature of the meat be at various points in the cooking process? I had to take a thermodynamics, fluids, and heat transfer course in college, so I decided to finally use that knowledge! As it turns out, meat cooking in a smoker can be fairly accurately modeled by basic heat transfer equations, exciting!
A Crash Course on Heat Transfer
I am by no means an expert on heat transfer, but the basic principles are pretty easy to understand.
The second law of thermodynamics says, in simple terms, that when two bodies at different temperatures interact, then heat is transferred from the warmer body to the colder body until they both reach the same temperature, known as thermal equilibrium.
In many cases of heat transfer in the real world, some object is placed into a larger environment where the temperature is different. In the case of smoking a pork shoulder, a (cold) pork shoulder is put into a (hot) smoker, and the smoker transfers heat into the pork shoulder. If the pork shoulder was left in the smoker for a long period of time, and the smoker had sufficient fuel such that it never changed temperature, then the pork shoulder would eventually reach the temperature of the smoker (or get pretty close).
Warning: Math Lies Ahead
The fundamental heat transfer equation is known as Newton's Law of Cooling, which is applicable for convective heat transfer (such is the case for our smoked pork shoulder example).
In terms of the temperature of the smaller body (pork shoulder) and the environmental temperature, it becomes a first order separable differential equation expressed as:
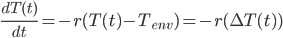
To solve this equation in order to get the temperature of the meat as a function of time, we must rearrange it a little bit.
First, multiply each side of the equation by dt and divide by 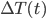 .
.
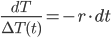
Then, integrate each side:
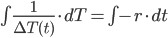
If you recall, the integral of 1/x results in ln(x), so we have:
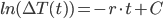
Solve for 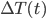 by taking both sides to the power of e...
by taking both sides to the power of e...
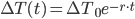
Substituting 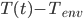 for
for 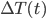 and solving, we are left with:
and solving, we are left with:
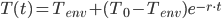
So there we have it, a pretty simple equation with only a few variables (well, for now at least).
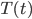 : The temperature of an object in a larger environment as a function of time elapsed in the environment. The pork shoulder, in our example.
: The temperature of an object in a larger environment as a function of time elapsed in the environment. The pork shoulder, in our example.
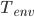 : The temperature of the environment, which would be the smoker temperature in our example.
: The temperature of the environment, which would be the smoker temperature in our example.
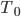 : The initial temperature of the object. In the case of a pork shoulder that you took out of the fridge, it would be approximately the temperature of the fridge, which is between 32 and 40 degrees Fahrenheit.
: The initial temperature of the object. In the case of a pork shoulder that you took out of the fridge, it would be approximately the temperature of the fridge, which is between 32 and 40 degrees Fahrenheit.
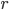 : A constant that determines at what rate the object will exponentially approach the environmental temperature. This is the tricky variable that we will discuss more later.
: A constant that determines at what rate the object will exponentially approach the environmental temperature. This is the tricky variable that we will discuss more later.
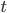 The time elapsed in the environment. Can be any units of time as long as they are consistent with the 'r' parameter.
The time elapsed in the environment. Can be any units of time as long as they are consistent with the 'r' parameter.
When you look at the solved form of the heat transfer equation, you can see that as time approaches infinity, the right portion of the equation goes to zero and the temperature of the object becomes the temperature of the environment, i.e. "thermal equilibrium". So, if you are really patient, you can set your smoker temperature to be the final desired doneness temperature of the meat, and you can't overcook it! This, however, takes a long time as we will see.
Variables That Affect How Quickly The Meat Cooks
If you were to place a metal sphere into your smoker, its temperature would increase at a different rate than a pork shoulder. This is due to a few factors:
Surface Area (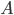 ): The area over which heat is contacting the meat will affect how quickly that heat gets inside the meat. If the meat is sitting atop a grill grate inside a covered smoker, then you can make a reasonable approximation that the meat is being hit with convective heat across its entire physical surface area. Basically, the more of the meat's surface that is exposed to the heat, the faster it will cook.
): The area over which heat is contacting the meat will affect how quickly that heat gets inside the meat. If the meat is sitting atop a grill grate inside a covered smoker, then you can make a reasonable approximation that the meat is being hit with convective heat across its entire physical surface area. Basically, the more of the meat's surface that is exposed to the heat, the faster it will cook.
Calculating surface area can either be a trivial matter that anyone who has taken math at above a 4th grade level should be able to do, or it can be enormously complicated and require complex modeling software and a powerful computer. Unfortunately, most shapes that we encounter in the real world (such as our pork shoulder) fall into the latter category, but in most cases we can make some approximations that they are pretty close to simpler shapes whose surface areas we can easily calculate. A pork shoulder can be approximated as either a rectangular prism, a cylinder, or a triangular prism, depending on how it is cut.
Mass (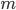 ): The mass of an object will determine how quickly heat is transferred into or out of it. In general, the more massive the object, the more slowly it changes temperature.
): The mass of an object will determine how quickly heat is transferred into or out of it. In general, the more massive the object, the more slowly it changes temperature.
Specific Heat Capacity (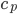 ): A measure of how much heat can be transferred to an object before it changes temperature. Will depend on the physical properties of the object. I was able to find this handy table that has specific heat capacities for a variety of foods. They have pork shoulder listed at 0.59 BTU/( lb oF).
): A measure of how much heat can be transferred to an object before it changes temperature. Will depend on the physical properties of the object. I was able to find this handy table that has specific heat capacities for a variety of foods. They have pork shoulder listed at 0.59 BTU/( lb oF).
Heat Transfer Coefficient (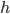 ): Number that characterizes how heat is transferred to an object that includes both the properties of the object as well as the nature of the heat transfer. Convective heat transfer through a medium of air will be different than conductive heat transfer using metal, for example. This was a tricky one to research as it can get pretty complicated, but based on this paper it seems to be somewhere between 5.1 and 9.1 W/(m^2 K). My model worked best when I used 12 (granted the paper was for processed ham and not pork shoulder).
): Number that characterizes how heat is transferred to an object that includes both the properties of the object as well as the nature of the heat transfer. Convective heat transfer through a medium of air will be different than conductive heat transfer using metal, for example. This was a tricky one to research as it can get pretty complicated, but based on this paper it seems to be somewhere between 5.1 and 9.1 W/(m^2 K). My model worked best when I used 12 (granted the paper was for processed ham and not pork shoulder).
Putting these variables together, we can derive a formula for r, the rate of heat transfer from the heat transfer equation:
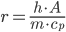
In this formula, the only things that will vary between pork shoulders are the mass and surface area.
Calculating Surface Area
If we make a few assumptions, then you can calculate the surface area of a pork shoulder by only knowing how much it weighs! The first assumption to make is that the pork shoulder will be of uniform density. This is not entirely accurate, but should be close enough.
The second assumption involves what shape the pork shoulder is, and its relative dimensions. The shape that seemed to work the best in my model is that of a triangular prism whose length is twice the height. Based on pork shoulders I've seen, this should be fairly close.
So, how do you determine surface area if all you know is weight (or, more precisely, mass...all of the equations are only valid on Earth...so be careful if you want to smoke a pork shoulder on the moon)? Well, if we assume constant density, 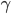 , then we can calculate the volume:
, then we can calculate the volume:
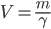
For pork shoulder, I've assumed a density of 0.0336 lb/in^3. Once we know the volume, then we can take a few liberties to figure out the surface area. The volume of a triangular prism is equal to:
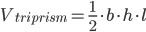
Where 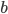 is the base of the triangle,
is the base of the triangle, 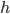 is the height of the triangle, and
is the height of the triangle, and 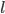 is the length of the prism. If we assume that it is an equilateral triangle with a length that is twice the height, then the volume equation becomes:
is the length of the prism. If we assume that it is an equilateral triangle with a length that is twice the height, then the volume equation becomes:
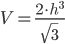
Once we back-calculate the height of the triangle based on the volume and the above equation, we can calculate surface area as:
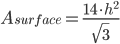
All right! We now can plug in all of the necessary parameters for 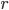 , knowing only what the mass (weight) of the pork shoulder is. Let's see what happens when we plug the numbers in.
, knowing only what the mass (weight) of the pork shoulder is. Let's see what happens when we plug the numbers in.
Cooking Times and Temperatures for Pork Shoulders of Various Weight
Whew, if you've made it this far, then you have bravely traversed all the math stuff...or just skipped it. If the former, then I applaud you.
Let's first look at the scenario in which my father and I cooked our pork: in a 275 degree Fahrenheit smoker.
As you can see from Fig. 1, pork shoulders of fairly standard weights can be cooked between 6 and 8 hours in a 275 degree smoker to a doneness temperature of 190 degrees (recommended for fall-apart tender pork shoulder). Another thing to note is that the meat temperature reaches the "halfway point" of doneness after only 3 hours of cooking, as the meat does not follow a linear temperature increase. So, if you are monitoring the meat temperature and early on in the cooking process feel like the temperature is increasing too rapidly, don't worry, it's supposed to do that.
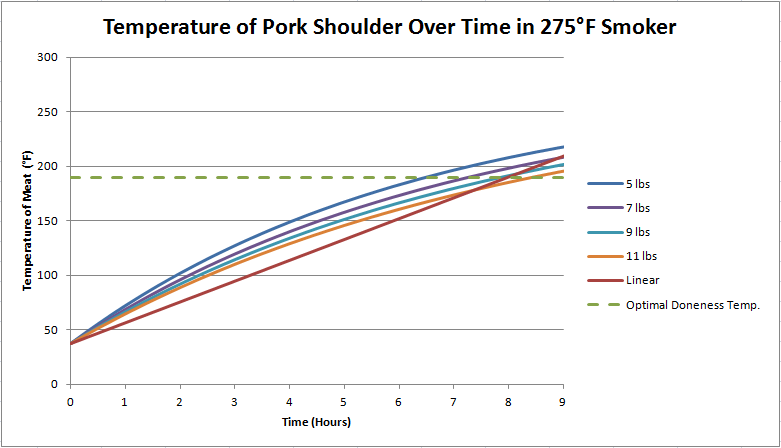
Now let's look at a scenario where we cook the pork in a 225 degree smoker. Obviously, it will take longer to reach desired doneness.
As you can see in Fig. 2, the time it will take the shoulder to cook at 225 degrees also varies based on weight, being between 11 and 13 hours for shoulder weights between 5 and 11 pounds.
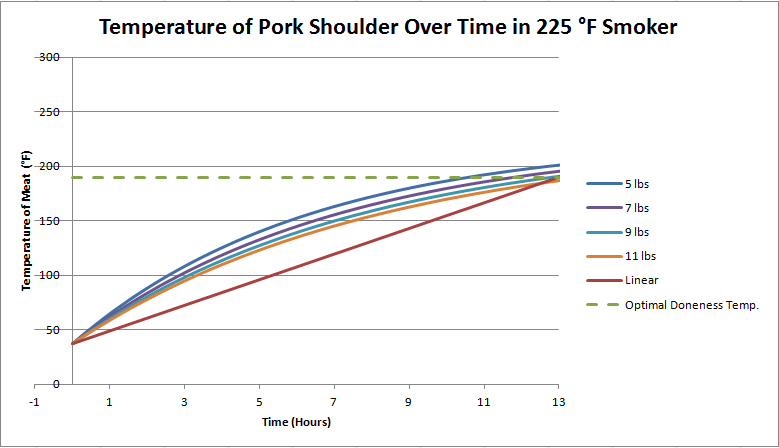
Now, what if we dropped the smoker temperature to 190 degrees, the desired doneness temperature of the meat?
An astute mathematical observer will note that the meat will actually never reach 190 degrees if the smoker is kept at exactly 190 degrees, but it will get pretty close, as you can see in Fig. 3. You can also note that it will increase in temperature fairly quickly, but after about 12 hours temperature increases become painfully slow. After 24 hours, you can pretty much call it "done".
Conclusion
Long story short, meat cooked over a relatively low temperature in a smoker will not experience a linear increase in internal temperature, so don't be worried if after a couple hours you think your meat is getting too hot too fast...that's just thermodynamics.
There ya go, if you thought your hobby (or business) of smoking pork butts was exempt from calculus and differential equations, then you were sadly mistaken.



Amazing! So cool!